T.P N° 2
"Compuertas"
1_ Para las compuertas AND, OR y EXOR de 2, 3 y 4 entradas las funcion y el símbolo y la tabla de verdad.
2_ Para el inversor la funcion, el símbolo y la tabla de verdad.
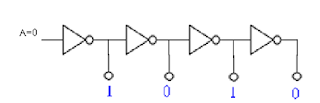
3_ Pasar el siguiente circuito indicar el valor de la variable A en cada punto.

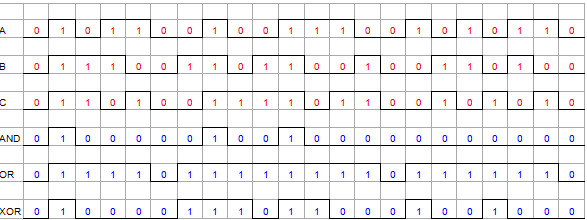
4_ Los siguientes trenes de pulsos están referidos a las compuertas AND, OR y EXOR de 3 entradas dibujar los trenes de pulsos o las salidas de cada una de ellas.
5_ Para las compuertas NAND, NOR y EXNOR de 3 entradas da la funcion el símbolo y la tabla de verdad.
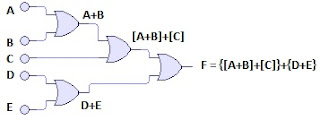
6_ Para el siguiente circuito obtener la funcion y la tabla de verdad.
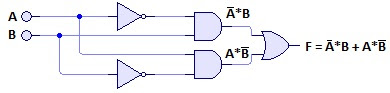
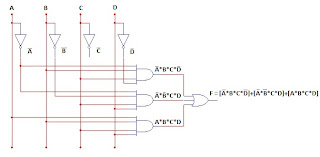
7_ Para los siguientes circuitos obtener la función y la tabla de verdad.
8_ Construir una funcion Or de 5 entradas utilizando solamente compuertas OR de 2 entradas.
9_ Para las siguientes funciones dar la tabla de verdad y el circuito.
A_ F=A*B*+A.B B_ F= AB**(+).C C_ F= A*BCD*+AB**CD+ABCD
10_ Verificar mediante tablas de verdad las leyes de morgan. Dibujar los circuitos
A_ A+B**=A*.B* B_ A.B**= A*+B*
11_ Completar las siguientes identidades verificar mediante. Tabla de verdad.

7_ Para los siguientes circuitos obtener la función y la tabla de verdad.
8_ Construir una funcion Or de 5 entradas utilizando solamente compuertas OR de 2 entradas.
9_ Para las siguientes funciones dar la tabla de verdad y el circuito.
A_ F=A*B*+A.B B_ F= AB**(+).C C_ F= A*BCD*+AB**CD+ABCD
10_ Verificar mediante tablas de verdad las leyes de morgan. Dibujar los circuitos
A_ A+B**=A*.B* B_ A.B**= A*+B*
11_ Completar las siguientes identidades verificar mediante. Tabla de verdad.
A_ A+A= F_ A.A=
B_ A+A*= G_ A.A*=
C_ A+A**= H_ A.A**=
D_ A+0= I_ A.0=
E_ A+1= J_ A.1=
12_ Buscar el pinout de todos los circuitos integrados de las familias CMOS y TTL que tengan solamente compuertas e inversores
Respuestas
1Y5_
AND
Tabla de verdad
Función
S=A*B
AND 3 ENTRADAS
Símbolo
Tabla de verdad
Funcion
S=A*B*C
AND 4 ENTRADAS
Simbolo
Tabla de verdad
Funcion
S=A*B*C*D
NAND 3 ENTRADAS
Simbolo
Tabla de verdad
Funcion
OR 2 ENTRADAS
Simbolo
Tabla de verdad
Funcion
S=A+B
OR 3 ENTRADAS
Simbolo
Tabla de verdad
Funcion
S=A+B+C
OR 4 ENTRADAS
Simbolo
Tabla de verdad
Funcion
S=A+B+C+D
NOR 3 ENTRADAS
Simbolo
Tabla de verdad
Funcion
Ŝ=A+B+C
XOR DE 2 ENTRADAS.
Simbolo
Tabla de verdad
Funcion
S=A(+)B
XOR DE 3 ENTRADAS
Simbolo
Tabla de verdad
Funcion
S=A(+)B(+)C
EXOR 4 ENTRADAS
Simbolo
Tabla de verdad
Funcion
S=A(+)B(+)C (+)D
Simbolo
Tabla de verdad
Funcion
Ŝ=A(+)B(+)C
Tabla de verdad
| A | B | S |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Función
S=A*B
AND 3 ENTRADAS
Símbolo
Tabla de verdad
| A | B | C | S |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
Funcion
S=A*B*C
AND 4 ENTRADAS
Simbolo
Tabla de verdad
| A | B | C | D | S |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 |
Funcion
S=A*B*C*D
NAND
NAND 3 ENTRADAS
Simbolo
Tabla de verdad
| A | B | C | S |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
Funcion
| Ŝ=A*B*C |
OR
OR 2 ENTRADAS
Simbolo
Tabla de verdad
| A | B | S |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Funcion
S=A+B
OR 3 ENTRADAS
Simbolo
Tabla de verdad
| A | B | C | S |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Funcion
S=A+B+C
OR 4 ENTRADAS
Simbolo
Tabla de verdad
| A | B | C | D | S |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
Funcion
S=A+B+C+D
NOR
NOR 3 ENTRADAS
Simbolo
Tabla de verdad
| A | B | C | S |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 |
Funcion
Ŝ=A+B+C
XOR
XOR DE 2 ENTRADAS.
Simbolo
Tabla de verdad
| A | B | S |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Funcion
S=A(+)B
XOR DE 3 ENTRADAS
Simbolo
Tabla de verdad
| A | B | C | S |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
Funcion
S=A(+)B(+)C
EXOR 4 ENTRADAS
Simbolo
Tabla de verdad
| A | B | C | D | S |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 0 |
Funcion
S=A(+)B(+)C (+)D
XNOR
XNOR 3 ENTRADASSimbolo
Tabla de verdad
| A | B | C | S |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
Funcion
Ŝ=A(+)B(+)C
2_
Simbolo
Tabla de verdad
| A | S |
| 0 | 1 |
| 1 | 0 |
Funcion
Ŝ=A
4_
6_
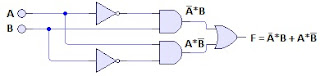
8_
D_
TTL:

A
|
B
|
AA*'B
|
'A*B + A*'B
| |||
0
|
0
|
1
|
1
|
0
|
0
|
0
|
0
|
1
|
1
|
0
|
1
|
0
|
1
|
1
|
0
|
0
|
1
|
0
|
1
|
1
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
7_
A
|
B
|
'A
|
'B
|
'A*'B
|
A*B
|
'A*'B + A*B
|
0
|
0
|
1
|
1
|
1
|
0
|
1
|
0
|
1
|
1
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
1
|
0
|
0
|
0
|
1
|
1
|
0
|
0
|
0
|
1
|
1
|
A
|
B
|
C
|
A(+)B
|
A*C
|
[A(+)B] + [A*C]
|
0
|
0
|
0
|
1
|
0
|
1
|
0
|
0
|
1
|
1
|
0
|
1
|
0
| 1 |
0
|
0
|
0
|
0
|
0
| 1 |
1
|
0
|
0
|
0
|
1
| 0 |
0
|
0
|
0
|
0
|
1
| 0 |
1
|
0
|
1
|
1
|
1
|
1
|
0
|
1
|
0
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
A
|
B
|
C
|
“A*B”
|
“A*B” + C
|
0
|
0
|
0
|
1
|
1
|
0
|
0
|
1
|
1
|
1
|
0
|
1
|
0
|
1
|
1
|
0
|
1
|
1
|
1
|
1
|
1
|
0
|
0
|
1
|
1
|
1
|
0
|
1
|
1
|
1
|
1
|
1
|
0
|
0
|
0
|
1
|
1
|
1
|
0
|
1
|
A
|
B
|
C
|
D
|
'A
|
'B
|
'C
|
'D
|
A*B*C*D
|
'A*B*'C*D
|
'A*'B*'C*'D
|
A*B*C*D + 'A*B*'C*D + 'A*'B*'C*'D
|
0
|
0
|
0
|
0
|
1
|
1
|
1
|
1
|
0
|
0
|
1
|
1
|
0
|
0
|
0
|
1
|
1
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
1
|
1
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
1
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
1
|
0
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
1
|
1
|
0
|
1
|
0
|
0
|
1
|
0
|
1
|
0
|
1
|
1
|
0
|
1
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
1
|
1
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
1
|
1
|
1
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
1
|
0
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
1
|
0
|
0
|
1
|
0
|
1
|
0
|
0
|
0
|
0
|
1
|
0
|
1
|
1
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
1
|
0
|
0
|
0
|
0
|
1
|
1
|
0
|
0
|
0
|
0
|
1
|
1
|
0
|
1
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
1
|
1
|
1
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
1
|
1
|
1
|
1
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
1
|
8_
9_
A_
A
|
B
|
'A
|
'B
|
'A*'B
|
A*B
|
'A*'B + A*B
|
0
|
0
|
1
|
1
|
1
|
0
|
1
|
0
|
1
|
1
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
1
|
0
|
0
|
0
|
1
|
1
|
0
|
0
|
0
|
1
|
1
|
B_
A
|
B
|
C
|
'A
|
'B
|
“A*B”
|
“A*B” (+) C
|
0
|
0
|
0
|
1
|
1
|
1
|
1
|
0
|
0
|
1
|
1
|
1
|
1
|
0
|
0
|
1
|
0
|
1
|
0
|
0
|
0
|
0
|
1
|
1
|
1
|
0
|
0
|
1
|
1
|
0
|
0
|
0
|
1
|
0
|
0
|
1
|
0
|
1
|
0
|
1
|
0
|
1
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
1
|
1
|
1
|
0
|
0
|
0
|
0
|
C_
A
|
B
|
C
|
'A
|
“A*B”
|
“A*B” + A
|
[“A*B” + A] + C
|
0
|
0
|
0
|
1
|
1
|
1
|
1
|
0
|
0
|
1
|
1
|
1
|
1
|
1
|
0
|
1
|
0
|
1
|
0
|
1
|
1
|
0
|
1
|
1
|
1
|
0
|
1
|
1
|
1
|
0
|
0
|
0
|
1
|
1
|
1
|
1
|
0
|
1
|
0
|
1
|
1
|
1
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
1
|
1
|
1
|
0
|
0
|
0
|
1
|
D_
A
|
B
|
C
|
D
|
'A
|
'B
|
'C
|
'D
|
'A*B*C*'D
|
'A*'B*C*D
|
A*B*C*D
|
'A*B*C*'D + 'A*'B*C*D + A*B*C*D
|
0
|
0
|
0
|
0
|
1
|
1
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
1
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
1
|
1
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
1
|
1
|
1
|
0
|
0
|
0
|
1
|
0
|
1
|
0
|
1
|
0
|
0
|
1
|
0
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
1
|
1
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
1
|
0
|
1
|
0
|
0
|
1
|
1
|
0
|
0
|
1
|
0
|
1
|
1
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
1
|
1
|
1
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
1
|
0
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
1
|
0
|
0
|
1
|
0
|
1
|
0
|
0
|
0
|
0
|
1
|
0
|
1
|
1
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
1
|
0
|
0
|
0
|
0
|
1
|
1
|
0
|
0
|
0
|
0
|
1
|
1
|
0
|
1
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
1
|
1
|
1
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
1
|
1
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
1
|
10_
"A+B" = 'A * 'B
A
|
B
|
'A
|
'B
|
"A+B"
|
'A*'B
|
0
|
0
|
1
|
1
|
1
|
1
|
0
|
1
|
1
|
0
|
0
|
0
|
1
|
0
|
0
|
1
|
0
|
0
|
1
|
1
|
0
|
0
|
0
|
0
|
"A*B"= 'A + 'B
A
|
B
|
'A
|
'B
|
"A*B
|
'A+'B
|
0
|
0
|
1
|
1
|
1
|
1
|
0
|
1
|
1
|
0
| 1 |
1
|
1
|
0
|
0
|
1
| 1 | 1 |
1
|
1
|
0
|
0
|
0
|
0
|
11_
A) F = A + A
A) F = A + A
B) F = A + 'A
A
|
A + 'A
|
0
| 1 |
| 1 | 1 |
C) F = "A + A"
D) F = A + 0
A
| A + 0 |
0
|
0
|
| 1 |
1
|
E) F = A + 1
A
|
A + 1
|
0
| 1 |
| 1 |
1
|
F) F = A * A
A
|
A * A
|
0
|
0
|
| 1 |
1
|
G) F = A * 'A
A
|
A * 'A
|
0
|
0
|
| 1 | 0 |
H) F = "A*A"
A
|
"A*A"
|
0
| 1 |
| 1 | 0 |
I) F = A * 0
A
|
A * 0
|
0
| 0 |
| 1 | 0 |
J) F = A * 1
A
|
A * 1
|
0
| 0 |
| 1 |
1
|
12_
CMOS:Quad 2-input gates
- 4001 quad 2-input NOR
- 4011 quad 2-input NAND
- 4030 quad 2-input EX-OR (now obsolete)
- 4070 quad 2-input EX-OR
- 4071 quad 2-input OR
- 4077 quad 2-input EX-NOR
- 4081 quad 2-input AND
Triple 3-input gates
- 4023 triple 3-input NAND
- 4025 triple 3-input NOR
- 4073 triple 3-input AND
- 4075 triple 3-input OR
Dual 4-input gates
- 4002 dual 4-input NOR
- 4012 dual 4-input NAND
- 4072 dual 4-input OR
- 4082 dual 4-input AND
Quad 2-input gates
- 7400 quad 2-input NAND
- 7403 quad 2-input NAND with open collector outputs
- 7408 quad 2-input AND
- 7409 quad 2-input AND with open collector outputs
- 7432 quad 2-input OR
- 7486 quad 2-input EX-OR
- 74132 quad 2-input NAND with Schmitt trigger inputs
Triple 3-input gates
- 7410 triple 3-input NAND
- 7411 triple 3-input AND
- 7412 triple 3-input NAND with open collector outputs
- 7427 triple 3-input NOR
Dual 4-input gates
- 7420 dual 4-input NAND
- 7421 dual 4-input AND